AG — Prof. Heiko Rieger — Statistical Physics

Statistical Physics

The statistical physics of systems far from equilibrium is still one of the most challenging fields in modern theoretical physics. Most natural systems, not only biological ones, are out of equilibrium. For instance the non-equilibrium dynamics in disordered systems takes place on enormously long time scales (in glasses theoretically even time scales of the order of the age of the universe) that it is called aging, which we studied intensively in the past. Currently we focus on random search processes and search strategies, pattern formation in ensembles of active particles, and imbibition and fluid flow in nano-porous media.

Current Research:

Optimal non-Markovian search strategies with n-step memory

Stochastic search processes are ubiquitous in nature and are expected to become more efficient when equipped with a memory, where the searcher has been before. A natural realization of a search process with long-lasting memory is a migrating cell that is repelled from the diffusive chemotactic signal that it secretes on its way, denoted as an autochemotactic searcher. To analyze the efficiency of this class of non Markovian search processes, we present a general formalism that allows one to compute the mean first passage time (MFPT) for a given set of conditional transition probabilities for non-Markovian random walks on a lattice. We show that the optimal choice of the n-step transition probabilities decreases the MFPT systematically and substantially with an increasing number of steps. It turns out that the optimal search strategies can be reduced to simple cycles defined by a small parameter set and that mirrorasymmetric walks are more efficient. For the autochemotactic searcher, we show that an optimal coupling between the searcher and the chemical reduces the MFPT to 1/3 of the one for a Markovian random walk.

Narrow escape problem in two-shell spherical domains

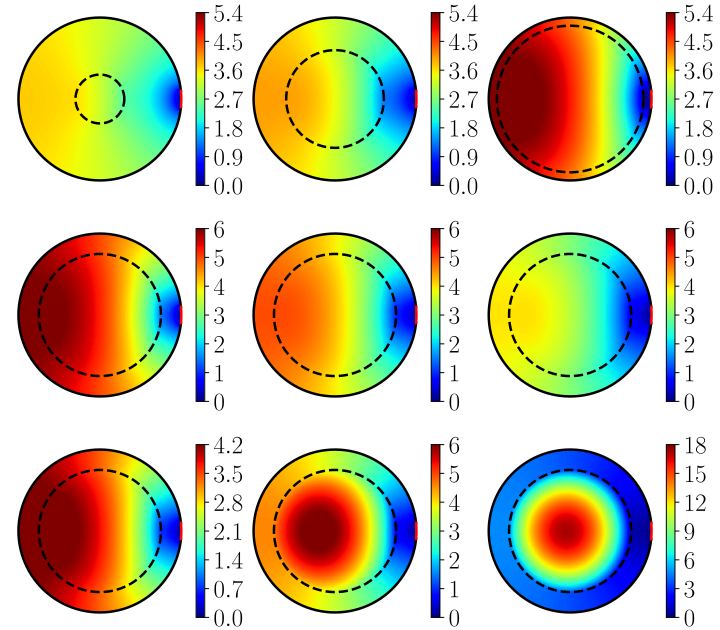
Intracellular transport in living cells is often spatially inhomogeneous with an accelerated effective diffusion close to the cell membrane and a ballistic motion away from the centrosome due to active transport along actin filaments and microtubules, respectively. Recently it was reported that the mean first passage time (MFPT) for transport to a specific area on the cell membrane is minimal for an optimal actin cortex width. In this paper, we ask whether this optimization in a two-compartment domain can also be achieved by passive Brownian particles. We consider a Brownian motion with different diffusion constants in the two shells and a potential barrier between the two, and we investigate the narrow escape problem by calculating the MFPT for Brownian particles to reach a small window on the external boundary. In two and three dimensions, we derive asymptotic expressions for the MFPT in the thin cortex and small escape region limits confirmed by numerical calculations of the MFPT using the finite-element method and stochastic simulations. From this analytical and numeric analysis, we finally extract the dependence of the MFPT on the ratio of diffusion constants, the potential barrier height, and the width of the outer shell. The first two are monotonous, whereas the last one may have a minimum for a sufficiently attractive cortex, for which we propose an analytical expression of the potential barrier height matching very well the numerical predictions.

Flocking with a q-fold discrete symmetry: band-to-lane transition in the active Potts model

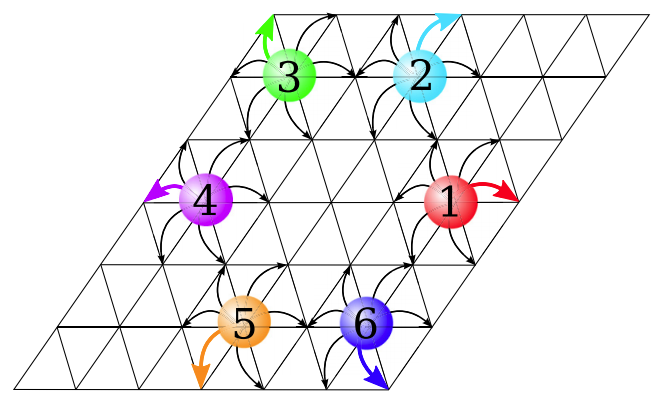
We study the q-state active Potts model (APM) on a two-dimensional lattice in which self-propelled particles have q internal states corresponding to the q directions of motion. A local alignment rule inspired by the ferromagnetic q-state Potts model and self-propulsion via biased diffusion according to the internal particle states elicits collective motion at high densities and low noise. We formulate a coarse-grained hydrodynamic theory with which we compute the phase diagrams of the APM for q = 4 and q = 6 and analyze the flocking dynamics in the coexistence region, where the high-density (polar liquid) phase forms a fluctuating stripe of coherently moving particles on the background of the low-density (gas) phase. A reorientation transition of the phase-separated profiles from transversal band motion to longitudinal lane formation is found, which is absent in the Vicsek model and the active Ising model. The origin of this reorientation transition is revealed by a stability analysis: for large velocities the transverse diffusivity approaches zero and stabilizes lanes. Computer simulations corroborate the analytical predictions of the flocking and reorientation transitions and validate the phase diagrams of the APM.

Capillary action in scalar active matter

We study the capacity of active matter to rise in thin tubes against gravity and other related phenomena, like, wetting of vertical plates and spontaneous imbibition, where a wetting liquid is drawn into a porous medium. This capillary action or capillarity is well known in classical fluids and originates from attractive interactions between the liquid molecules and the container walls, and from the attraction of the liquid molecules among each other. We observe capillarity in a minimal model for scalar active matter with purely repulsive interactions, where an effective attraction emerges due to slowdown during collisions between active particles and between active particles and walls. Simulations indicate that the capillary rise in thin tubes is approximately proportional to the active sedimentation length λ and that the wetting height of a vertical plate grows superlinear with λ. In a disordered porous medium the imbibition height scales as <h> ∝ λΦm, where Φm is its packing fraction.

Flocking and reorientation transition in the 4-state active Potts model

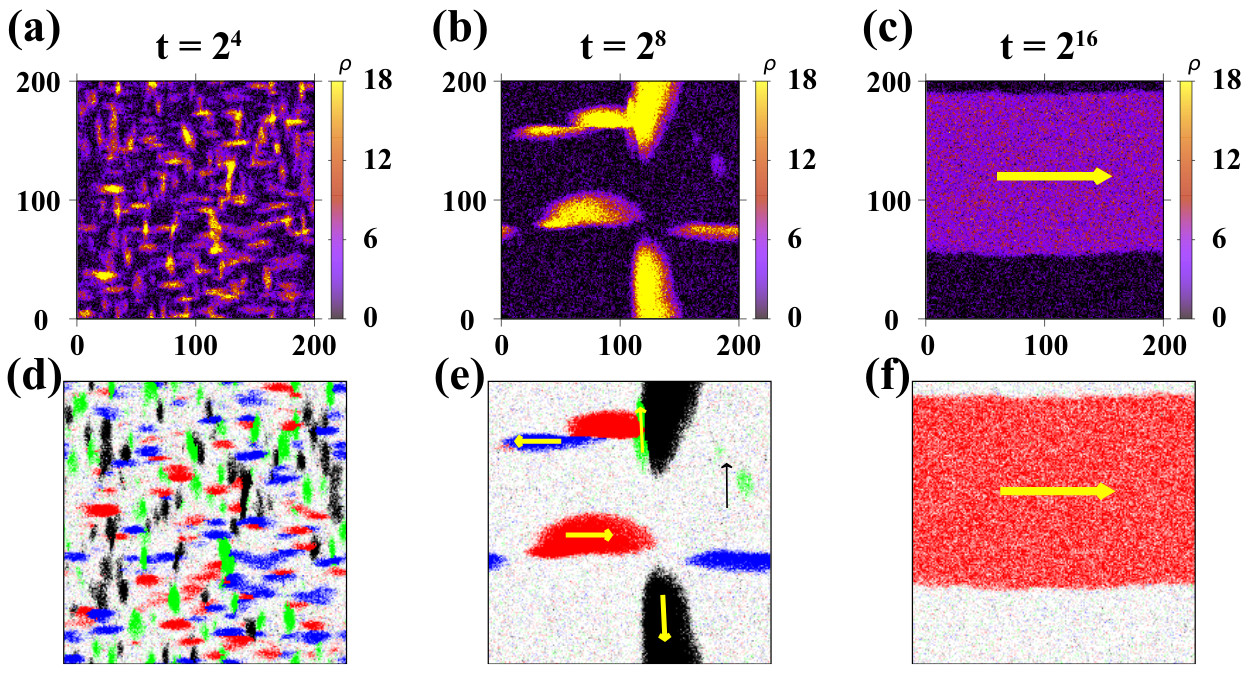
We study the active 4-state Potts model (APM) on the square lattice in which active particleshave four internal states corresponding to the four directions of motion. A local alignment rule in-spired by the ferromagnetic 4-state Potts model and self-propulsion via biased diffusion according tothe internal particle states leads to flocking at high densities and low noise. We compute the phasediagram of the APM and explore the flocking dynamics in the region, in which the high-density(liquid) phase coexists with the low-density (gas) phase and forms a fluctuating band of coherentlymoving particles. As a function of the particle self-propulsion velocity, a novel reorientation transi-tion of the phase-separated profiles from transversal to longitudinal band motion is revealed, whichis absent in the Vicsek model and the active Ising model. We further construct a coarse-grainedhydrodynamic description of the model which validates the results for the microscopic model.

Transient anomalous diffusion in run-and-tumble dynamics

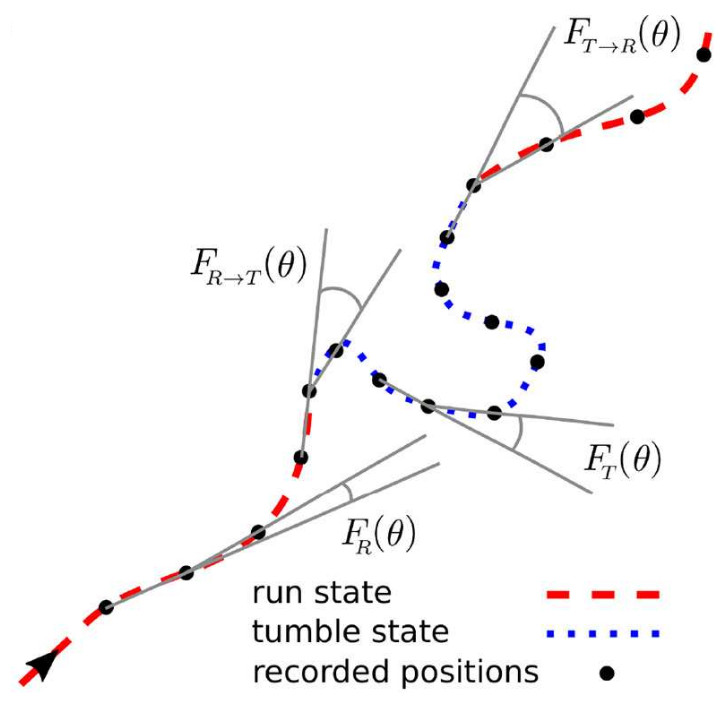
We study the stochastic dynamics of a particle with two distinct motility states. Each oneis characterized by two parameters: one represents the average speed and the otherrepresents the persistence quantifying the tendency to maintain the current direction ofmotion. We consider a run-and-tumble process, which is a combination of an activefast motility mode (persistent motion) and a passive slow mode (diffusion). Assumingstochastic transitions between the two motility states, wederive an analytical expressionfor the time evolution of the mean square displacement. The interplay of the keyparameters and the initial conditions as for instance the probability of initially starting inthe run or tumble state leads to a variety of transient regimes of anomalous transport ondifferent time scales before approaching the asymptotic diffusive dynamics. We estimatethe crossover time to the long-term diffusive regime and prove that the asymptoticdiffusion constant is independent of initially starting inthe run or tumble state.

The narrow escape problem in a circular domain with radial piecewise constant diffusivity

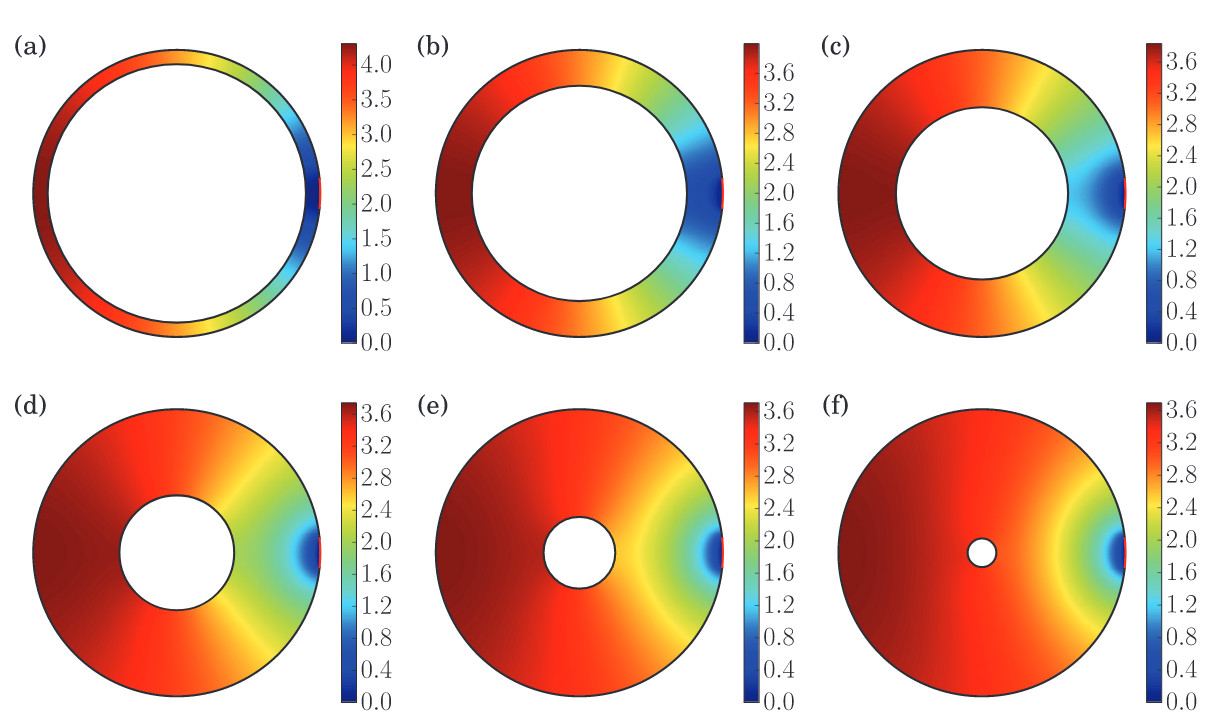
The stochastic motion of particles in living cells is often spatially inhomogeneous with a higher effective diffusivity in a region close to the cell boundary due to active transport along actin filaments. As a first step to understand the consequence of the existence of two compartments with different diffusion constant for stochastic search problems we consider here a Brownian particle in a circular domain with different diffusion constants in the inner and the outer shell. We focus on the narrow escape problem and compute the mean first passage time (MFPT) for Brownian particles starting at some pre-defined position to find a small region on the outer reflecting boundary. For the annulus geometry we find that the MFPT can be minimized for a specific value of the width of the outer shell. In contrast for the two-shell geometry we show that the MFPT depends monotonously on all model parameters, in particular on the outer shell width. Moreover we find that the distance between the starting point and the narrow escape region which maximizes the MFPT depends discontinuously on the ratio between inner and outer diffusivity.

Numerical analysis of homogeneous and inhomogeneous intermittent search strategies

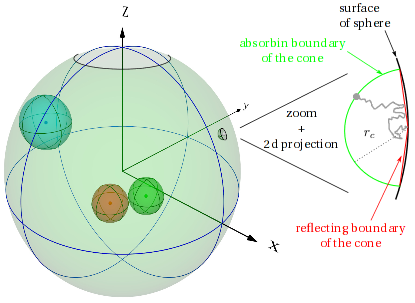
Random search processes for targets that are inhomogeneously distributed in a search domain require spatially inhomogeneous search strategies to find the target as fast as possible. Here we compare systematically the efficiency of homogeneous and inhomogeneous strategies for intermittent search, which alternates stochastically between slow, diffusive motion in which the target can be detected and fast ballistic motion during which targets cannot be detected. We analyze the mean first passage time (MFPT) of homogeneous and inhomogeneous strategies for three paradigmatic search problems: 1) the narrow escape problem, 2) reaction kinetics and 3) the reaction-escape problem. Using families of inhomogeneous strategies, partially motivated by the organization of the cytoskeleton in cells with a centrosome, we show that inhomogeneous strategies are almost always more efficient than homogeneous ones.

Meniscus Arrest during Capillary Rise in Asymmetric Microfluidic Pore Junctions

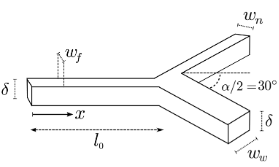
The capillary rise of liquid in asymmetric channel junctions with branches of different radii can lead to long-lasting meniscus arrests in the wider channel, which has important implications for the morphology and dynamical broadening of imbibition fronts in porous materials with elongated pores. Using a microfluidic setup, we experimentally demonstrate the existence of arrest events in Y-shaped junctions, and measure their duration and compare them with theoretical predictions. For various ratios of the channel width and liquid viscosities and for different values of the feeding channel length, we find that the meniscus within the wider branch is arrested for a time that is proportional to the time that the meniscus needed to reach the junction, in very good quantitative agreement with theoretical predictions.

Persistent-random-walk approach to anomalous transport of self-propelled particles

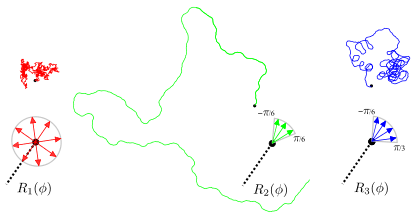
The motion of self-propelled particles is modeled as a persistent random walk. An analytical framework is developed that allows the derivation of exact expressions for the time evolution of arbitrary moments of the persistent walk’s displacement. It is shown that the interplay of step length and turning angle distributions and self-propulsion produces various signs of anomalous diffusion at short time scales and asymptotically a normal diffusion behavior with a broad range of diffusion coefficients. The crossover from the anomalous short-time behavior to the asymptotic diffusion regime is studied and the parameter dependencies of the crossover time are discussed. Higher moments of the displacement distribution are calculated and analytical expressions for the time evolution of the skewness and the kurtosis of the distribution are presented.

Propagating interfaces in mixtures of active and passive Brownian particles

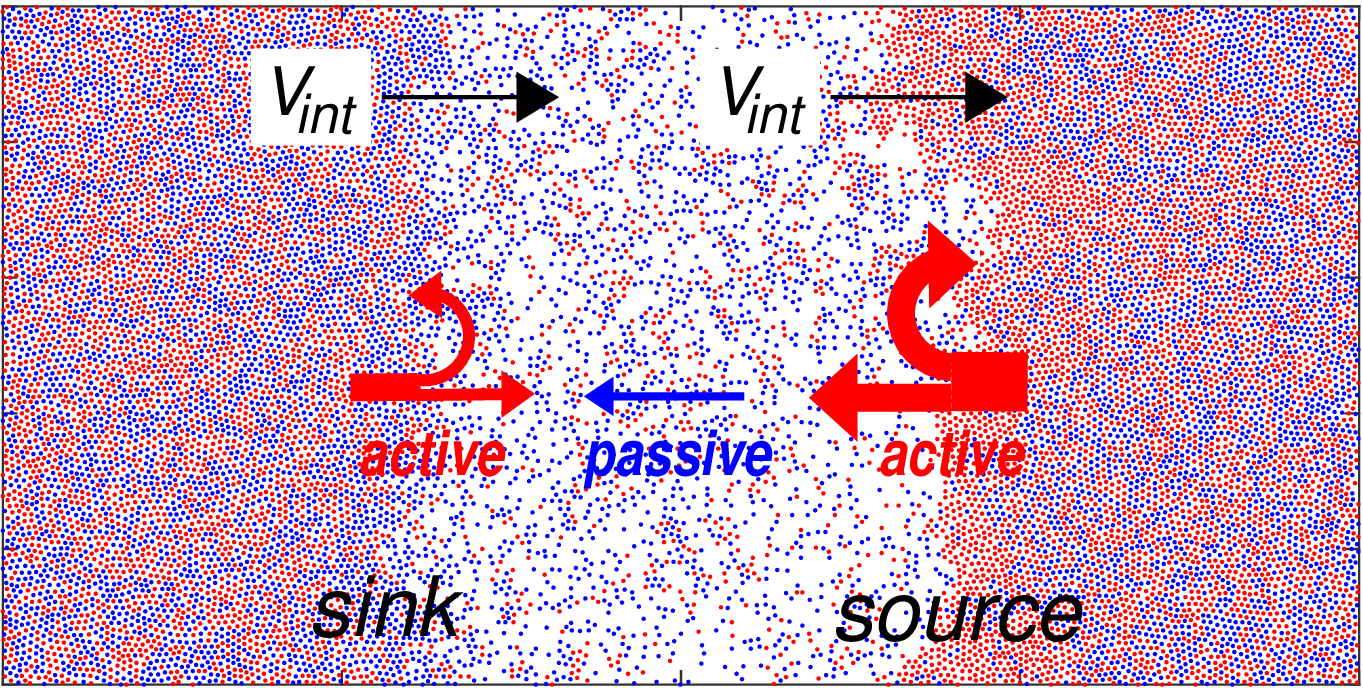
We study numerically the emergent collective dynamics in phase-separated mixtures of isometric active and passive Brownian particles in two dimensions. We find that these systems exhibit a novel and so far unexplored type of collective motion in the phase-separated state in the form of well-defined propagating interfaces, which can be either enriched or depleted of active particles, and are advancing toward or receding from the dense phase, respectively. The propagation arises due to flux imbalance at the interface, resembling the growth behavior of rough surfaces far from equilibrium.

Meniscus arrest dominated imbibition front roughening in porous media with elongated pores

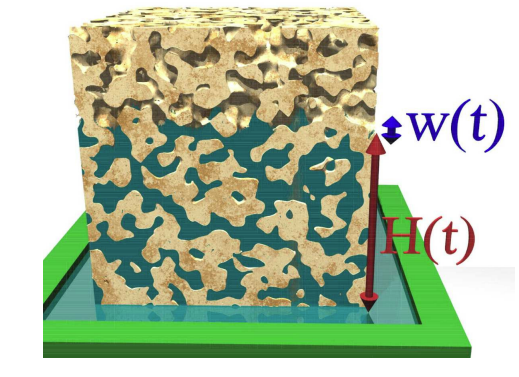
During spontaneous imbibition, a wetting liquid is drawn into a porous medium by capillary forces. Recently, anomalous scaling properties of front broadening during spontaneous imbibition of water in Vycor glass, a nanoporous medium, were reported. The mean height and the width of the propagating front increase with time t both proportional to t 1/2. We argue that this anomalously large roughening exponent of Β = 1/2 is due to long-lasting meniscus arrests, when at pore junctions the meniscus propagation in one or more branches comes to a halt when the Laplace pressure of the meniscus exceeds the hydrostatic pressure within the junction. From this hypothesis we derive the scaling relations for the emerging arrest time distribution in random pore networks and show that the average front width is proportional to the height yielding a roughness exponent of exactly Β = 1/2 as measured in the Vycor glass imbibition experiments. Extensive simulations of a random pore network model confirm these predictions. Finally, using a microfluidic setup as well as molecular dynamics simulations on the nanoscale, the basic hypothesis of the scaling theory is confirmed by demonstrating the existence of arrest events in Y-shaped junctions, analyzing them quantitatively and comparing them with the theoretical predictions.

Meniscus arrest dominated imbibition front roughening in porous media with elongated pores

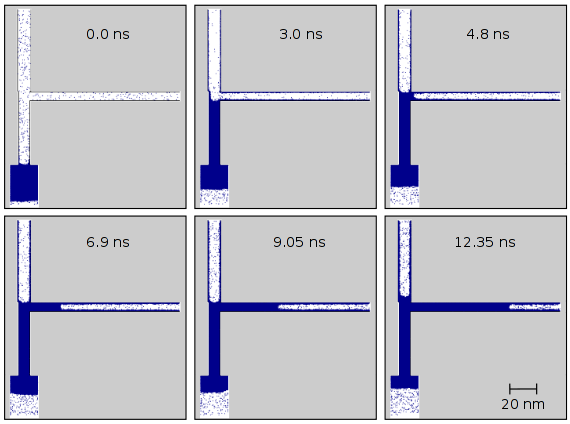
During spontaneous imbibition, a wetting liquid is drawn into a porous medium by capillary forces. Recently, anomalous scaling properties of front broadening during spontaneous imbibition of water in Vycor glass, a nanoporous medium, were reported. The mean height and the width of the propagating front increase with time t both proportional to t 1/2 . We argue that this anomalously large roughening exponent of Β = 1 / 2 is due to long-lasting meniscus arrests, when at pore junctions the meniscus propagation in one or more branches comes to a halt when the Laplace pressure of the meniscus exceeds the hydrostatic pressure within the junction. From this hypothesis we derive the scaling relations for the emerging arrest time distribution in random pore networks and show that the average front width is proportional to the height yielding a roughness exponent of exactly Β = 1 / 2 as measured in the Vycor glass imbibition experiments. Extensive simulations of a random pore network model confirm these predictions. Finally, using a micro uidic setup as well as molecular dynamics simulations on the nanoscale, the basic hypothesis of the scaling theory is confirmed by demonstrating the existence of arrest events in Y-shaped junctions, analyzing them quantitatively and comparing them with the theoretical predictions.

Anomalous Diffusion of Self-Propelled Particles in Directed Random Environments

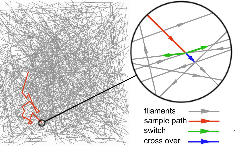
We theoretically study the transport properties of self-pr opelled particles on complex structures, such as motor proteins on filament networks. A general master equation formalism is developed to investigate the persistent motion of individual random w alkers, which enables us to identify the contributions of key parameters: the motor processivity, a nd the anisotropy and heterogeneity of the underlying network. We prove the existence of different dyna mical regimes of anomalous motion, and that the crossover times between these regimes as well as the asymptotic diffusion coefficient can be increased by several orders of magnitude within biologic ally relevant control parameter ranges. In terms of motion in continuous space, the interplay betwee n stepping strategy and persistency of the walker is established as a source of anomalous diffusion a t short and intermediate time scales which has not been considered so far.

Lattice Model for Spontaneous Imbibition in Porous Media: The Role of Effective Tension and Universality Class

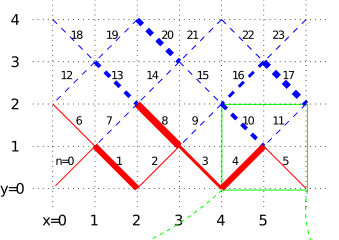
Recently, anomalous scaling properties of front broadening during spontaneous imbibition of water in Vycor glass, a nanoporous medium, were reported: the mean height and the width of the propagating front increase with time t both proportional to t 1/2 . Here, we propose a simple lattice imbibition model and elucidate quantitatively how the correlation range of the hydrostatic pressure and the disorder strength of the pore radii affect the scaling properties of the imbibition front. We introduce an effective tension of liquid across neighboring pores, which depends on the aspect ratio of each pore, and show that it leads to a dynamical crossover: both the mean height and the roughness grow faster in the presence of tension in the intermediate-time regime but eventually saturate in the long-time regime. The universality class of the long-time behavior is discussed by examining the associated scaling exponents and their relation to directed percolation.

Scaling Theory for Spontaneous Imbibition in Random Networks of Elongated Pores

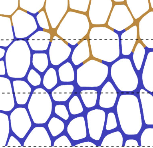
We present a scaling theory for the long time behavior of spontaneous imbibition in porous media consisting of interconnected pores with a large length-to-width ratio. At pore junctions, the meniscus propagation in one or more branches can come to a halt when the Laplace pressure of the meniscus exceeds the hydrostatic pressure within the junction. We derive the scaling relations for the emerging arrest time distribution and show that the average front width is proportional to the height, yielding a roughness exponent of exactly Β = 1/2 and explaining recent experimental results for nanoporous Vycor glass. Extensive simulations of a pore network model confirm these predictions.

Efficient kinetic Monte Carlo method for reaction-diffusion problems with spatially varying annihilation rates

We present an efficient Monte Carlo method to simulate reaction-diffusion processes with spatially varying particle annihilation or transformation rates. Like Green's function reaction dynamics and first-passage time methods, our algorithm avoids small diffusive hops by propagating sufficiently distant particles in large hops to the boundaries of protective domains. Since for spatially varying annihilation or transformation rates the single particle diffusion propagator is not known analytically, we present an algorithm that generates efficiently either particle displacements or annihilations with the correct statistics, as we prove rigorously. The numerical efficiency of the algorithm is demonstrated with an illustrative example.

Anomalous Front Broadening During Spontaneous Imbibition in a Porous Matrix with Elongated Pores

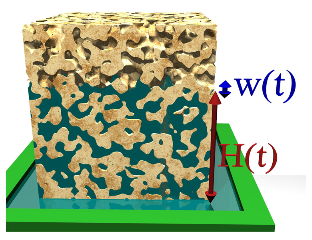
During spontaneous imbibition, a wetting liquid is drawn into a porous medium by capillary forces. In systems with comparable pore length and diameter, such as paper and sand, the front of the propagating liquid forms a continuous interface. Sections of this interface advance in a highly correlated manner due to an effective surface tension, which restricts front broadening. Here we investi- gate water imbibition in a nanoporous glass (Vycor) in which the pores are much longer than they are wide. In this case, no continuous liquid–vapor interface with coalesced menisci can form. Anomalously fast imbibition front roughening is experimentally observed by neutron imaging. We propose a theoretical pore-network model, whose structural details are adapted to the microscopic pore structure of Vycor glass and show that it displays the same large-scale roughening characteristics as observed in the experiment. The model predicts that menisci movements are uncorrelated, indicating that despite the connectivity of the network the smoothening effect of surface tension on the imbibition front roughening is negligible. These results suggest a new universality class of imbibition behavior, which is expected to occur in any matrix with elongated, interconnected pores of random radii.

Legal notice (Impressum) Privacy policy