AG — Prof. Heiko Rieger — Statistical Physics
Quantum phase transition and correlations in the multi-spin-boson model
Preface
In any physical situation, in which the involved action is that small, that it is comparable to the Planck constant, the intuitive classical picture of the every day life may be misleading. One enters the realm of quantum mechanics, where effects can take place, that are completely incompatible with classical mechanics. The world becomes quantized and probabilistic rather than continuous and deterministic.
In statistical physics, the quantum effects enters, if the temperature is lowered that much, that thermal action is of the order of the Planck constant. The quantum fluctuations will then compete or even dominate thermal fluctuations. In this case, the classical theory of phase transitions is altered. One speaks of quantum phase transitions, if a control parameter, that originates from a quantum property is used to drive a system through its transition, rather than the temperature.
The Spin-boson model
In the framework of quantum dissipation, one perturbates the quantum fluctuation by environmental influence. The idea behind that is to impose the concept of friction to the steady quantum motion. The probably most prominent archetype model of the class is the spin-boson model, that consists of a two-state system that couples to a continuous spectrum of bosonic bath modes. Although the model is discussed in literature for almost three decades, it is still part of current research. Our interest is the investigation of the equilibrium properties and the quantum phase transition of the spin-boson model and extensions to it. Our focus in on developing effective numerical methods to either explore unknown regimes or contribute high quality results to existing problems.
Quantum Monte Carlo cluster algorithm
Our Quantum Monte Carlo cluster algorithm 1 based on the path integral representation of the spin-boson hamiltonian and works completely in continuous imaginary time. This has several advantages:
- The use of the cluster scheme enables global Monte Carlo updates, that is strongly desirable to investigate continuous phase transitions
- Operating completely in continuous time eliminates any effort and uncertainties concerning the Trotter discretization
Current investigations
Currently we study spin-boson systems with multiple impurities in a common bath 2 of which the interesting feature is the mutual influence of the spins, even in the absence of a direct coupling between them. The common bath mediates in a non-trivial way between all the spins. Even more complexity enters the system, if one extends the model by the concept of spatial separation. With this extension, one has the distance as an additional parameter, the affects the spin-spin correlations and even the criticality of the system.
Figures
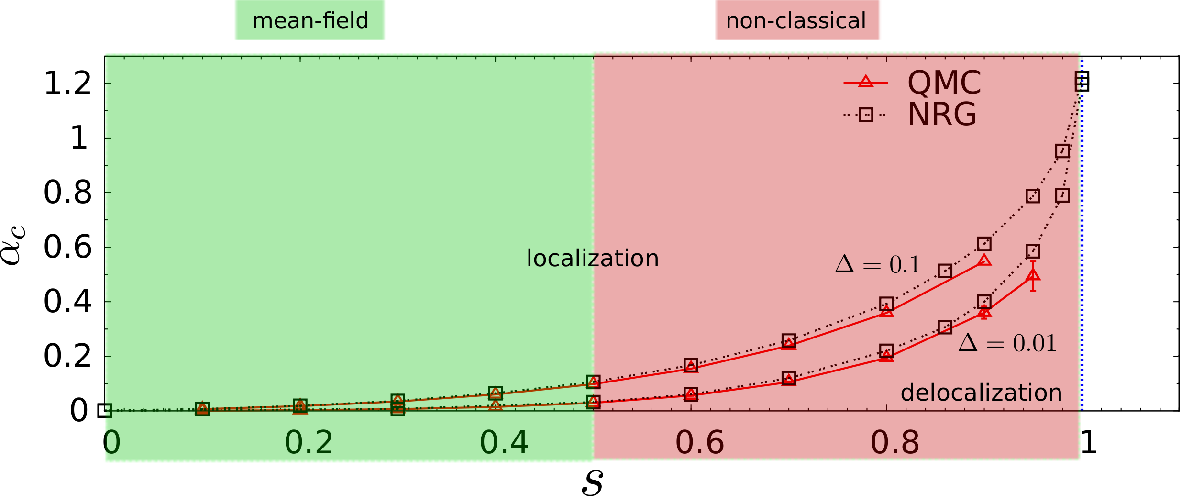
Figure 1: Phase diagram of the (sub-)Ohmic spin-boson model without bias. Data for 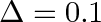 from 1.
from 1.
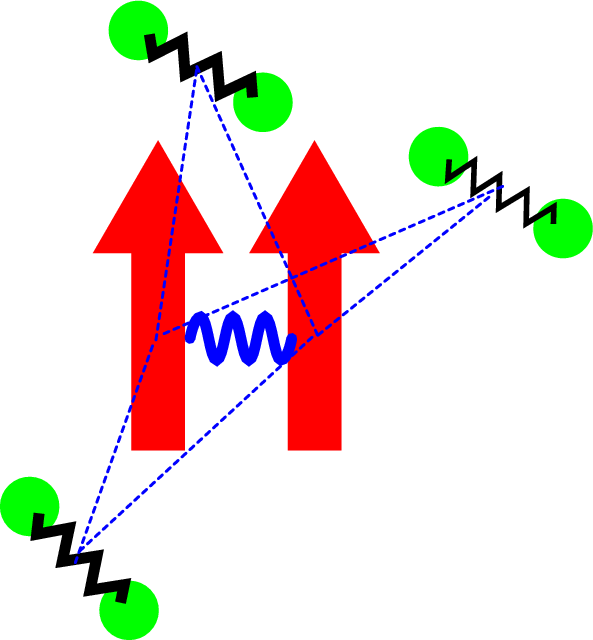
Figure 2: Sketch of the two-impurity spin-boson model. Both 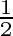 -spins are placed in a common bosonic bath,
that acts as a mediator between them.
-spins are placed in a common bosonic bath,
that acts as a mediator between them.
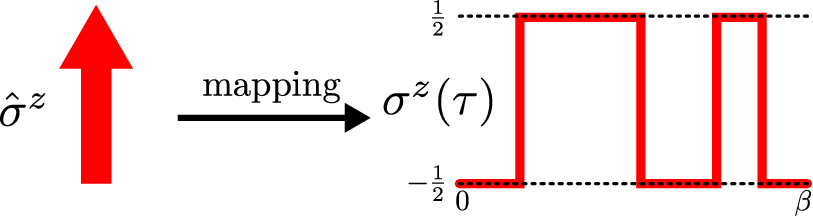
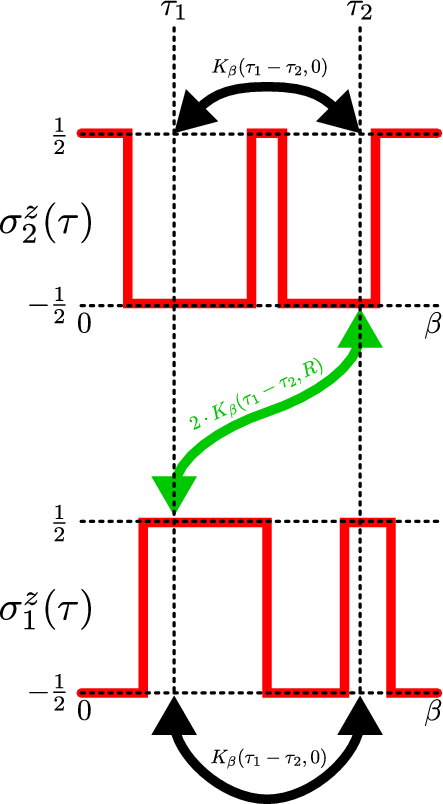
Figure 3: Sketch of the path integral representation of the two-impurity spin-boson model. (left) Within the path integral reformulation, a  -spin is represented as a continuous worldline
-spin is represented as a continuous worldline ![z σ (τ) : [0,β] → {- 1,1}](quantum_dissipation7x.png) . (right) Due to the dissipation, a long range interaction arises along the imaginary time axis (black arrows). For multiple spins embedded in the same environment, also cross actions (green arrow) have to take into account.
. (right) Due to the dissipation, a long range interaction arises along the imaginary time axis (black arrows). For multiple spins embedded in the same environment, also cross actions (green arrow) have to take into account.
References
| The quantum phase transition in the sub-ohmic spin-boson model: Quantum Monte-Carlo study with a continuous imaginary time algorithm |
|
| Phys. Rev. Lett. 102, 030601 (2009) | [cond-mat], [pdf] |
| Quantum phase transition and correlations in the multi-spin-boson model |
|
| Phys. Rev. B 90, 224401 (2014) | [pdf], [arXiv] |
Legal notice (Impressum) Privacy policy



