AG — Prof. Heiko Rieger — Statistical Physics

Statistical Physics (Quantum)

Quantum statistical physics is concerned with collective phenomena in systems with many quantum mechanical degrees of freedom (electrons, bosons, spins, qbits, etc). Paradigmatic examples, also studied in our research group, are quantum phase transitions, where macroscopic properties of a strongly inteacting quantum many body system change dramatically at zero temerature by tuning for instance an external field. Another example is the quantum relaxation of many particle systems after sudden changes of an external field, which is experimentally observable for instance in ultracold atoms in optical lattices. Important issues here are quantum thermalization and the growth of entanglement.

Current Research:

Haldane Insulator in the 1D Nearest-Neighbor Extended Bose-Hubbard Model with Cavity-Mediated Long-Range Interactions

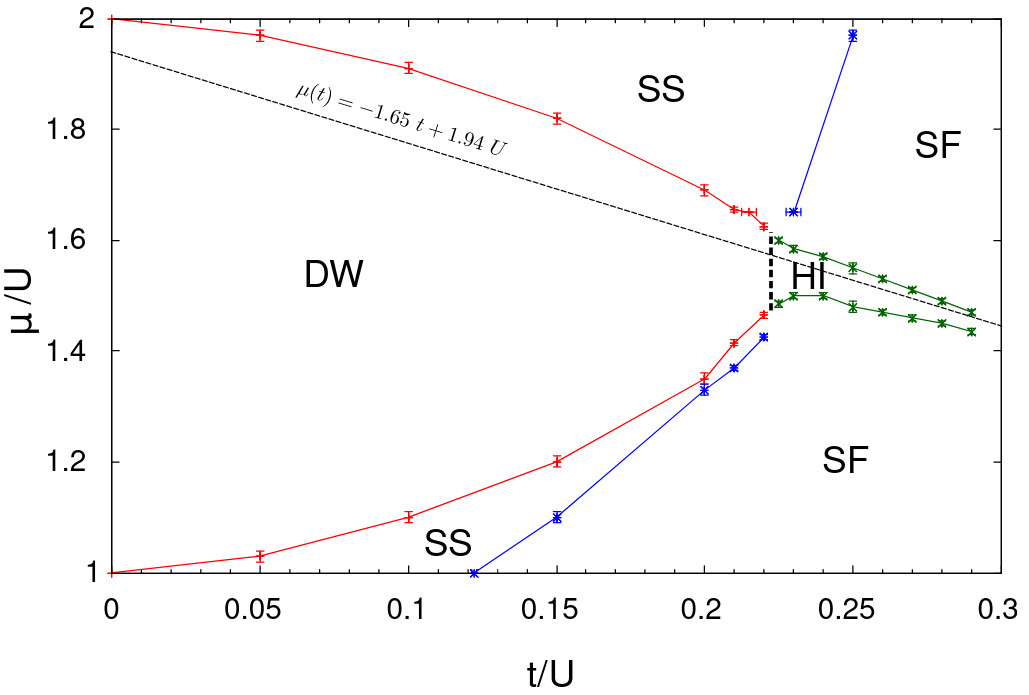
In the one-dimensional Bose-Hubbard model with on-site and nearest neighbor interactions, agapped phase characterized by an exotic non-local order parameter emerges, the Haldane insulator.Bose-Hubbard models with cavity-mediated global range interactions display phase diagrams, whichare very similar to those with nearest neighbor repulsive interactions, but the Haldane phase remainselusive there. Here we study the one-dimensional Bose-Hubbard model with nearest-neighbor andcavity-mediated global-range interactions and scrutinize the existence of a Haldane Insulator phase.With the help of extensive quantum Monte-Carlo simulations we find that in the Bose-Hubbardmodel with only cavity-mediated global-range interactions no Haldane phase exists. For a combi-nation of both interactions, the Haldane Insulator phase shrinks rapidly with increasing strength ofthe cavity-mediated global-range interactions. Thus, in spite of the otherwise very similar behaviorthe mean-field like cavity-mediated interactions strongly suppress the non-local order favored bynearest neighbor repulsion in some regions of the phase diagram.





Reentrant random quantum Ising antiferromagnet

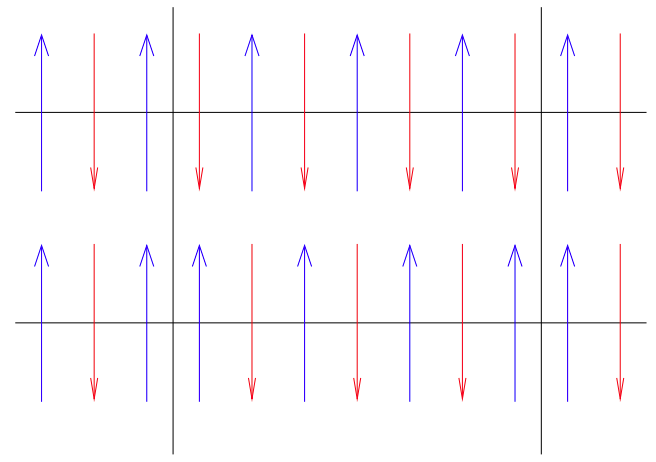
We consider the quantum Ising chain with uniformly distributed random antiferromagnetic couplings (1 ≤ Ji ≤ 2) and uniformly distributed random transverse fields (Γ0 ≤ Γi ≤ 2Γ0) in the presence of a homogeneous longitudinal field, h. Using different numerical techniques (density-matrix renormalization group, combinatorial optimization, and strong disorder renormalization group methods) we explore the phase diagram, which consists of an ordered and a disordered phase. At one end of the transition line h = 0, Γ0 = 1) there is an infinite disorder quantum fixed point, while at the other end (h = 2, Γ0 = 0) there is a classical random first-order transition point. Close to this fixed point, for h > 2 and Γ0 > 0 there is a reentrant ordered phase, which is the result of quantum fluctuations by means of an order through disorder phenomenon

The effect of disorder on the phase diagrams of hard-core lattice bosons with cavity-mediated long-range and nearest-neighbor interactions

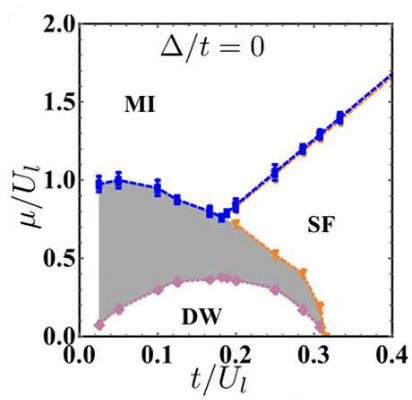
We use quantum Monte Carlo simulations with the worm algorithm to study the phasediagram of a two-dimensional Bose-Hubbard model with cavity-mediated long-rangeinteractions and uncorrelated disorder in the hard-core limit. Our study shows the systemis in a supersolid phase at weak disorder and a disordered solid phase at strongerdisorder. Due to long-range interactions, a large co-existregion of density-wave andMott insulator phases exists in both clean and disordered systems. By comparing thephase diagrams for both clean and disordered systems, we findthat disorder suppressessuperfluidity and narrows the co-exist region caused by firstorder phase transition. Wecompare these results with the phase diagram of the extendedBose-Hubbard modelwith nearest-neighbor interactions. Here, the supersolidphase does not exist even atweak disorder. We identify two kinds of glassy phases: a Boseglass phase and adisordered solid phase. The glassy phases intervene between the density-wave andsuperfluid phases as the Griffiths phase of the Bose-Hubbard model. The disorderedsolid phase intervenes between the density-wave and Bose glass phases since bothhave a finite structure factor.









Phase diagrams of the disordered Bose-Hubbard model with cavity-mediated long-range and nearest-neighbor interactions

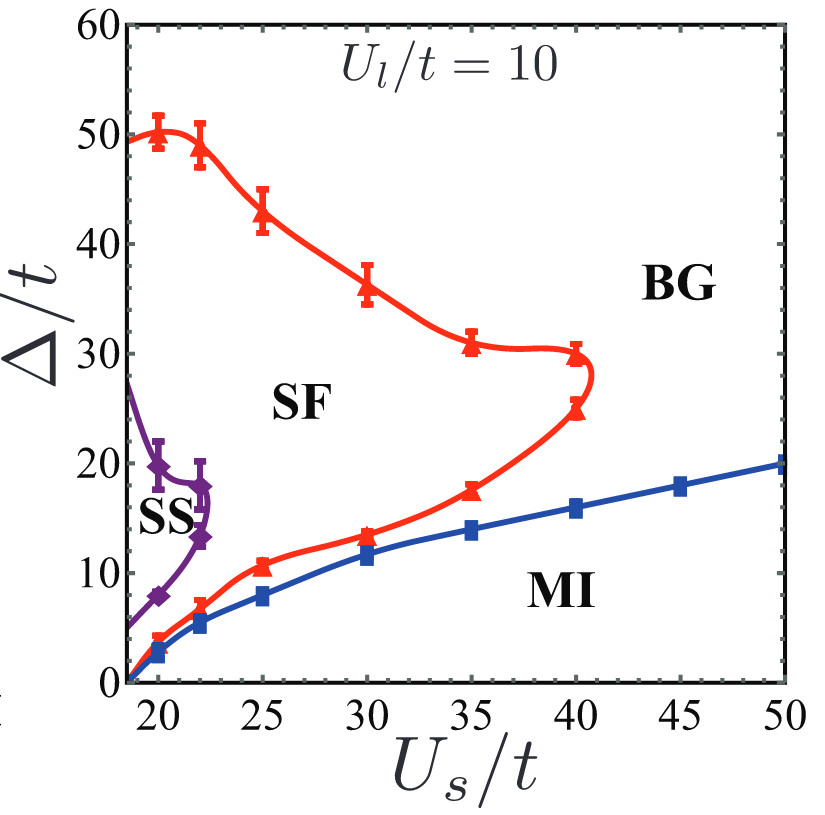
Recent experiments with ultracold atoms in an optical lattice have realized cavity-mediated long-range interaction and observed the emergence of a supersolid phase and a density wave phase in additionto Mott insulator and superfluid phases. Here we consider theoretically the effect of uncorrelated disorderon the phase diagram of this system and study the two-dimensional Bose-Hubbard model with cavity-mediated long-range interactions and uncorrelated diagonal disorder. We also study the phase diagramof the extended Bose-Hubbard model with nearest-neighbor interactions in the presence of uncorrelateddiagonal disorder. The extended Bose-Hubbard model with nearest-neighbor interactions has been realizedin the experiment using dipolar interaction recently. With the help of quantum Monte Carlo simulationsusing the worm algorithm, we determine the phase diagram of those two models. We compare the phasediagrams of cavity-mediated long-range interactions with nearest-neighbor interactions. We show that twokinds of Bose glass phases exist: one with and one without density wave order. We also find that weakdisorder enhances the supersolid phase.









Variational Monte-Carlo study of the extended Bose-Hubbard model with short- and infinite-range interactions

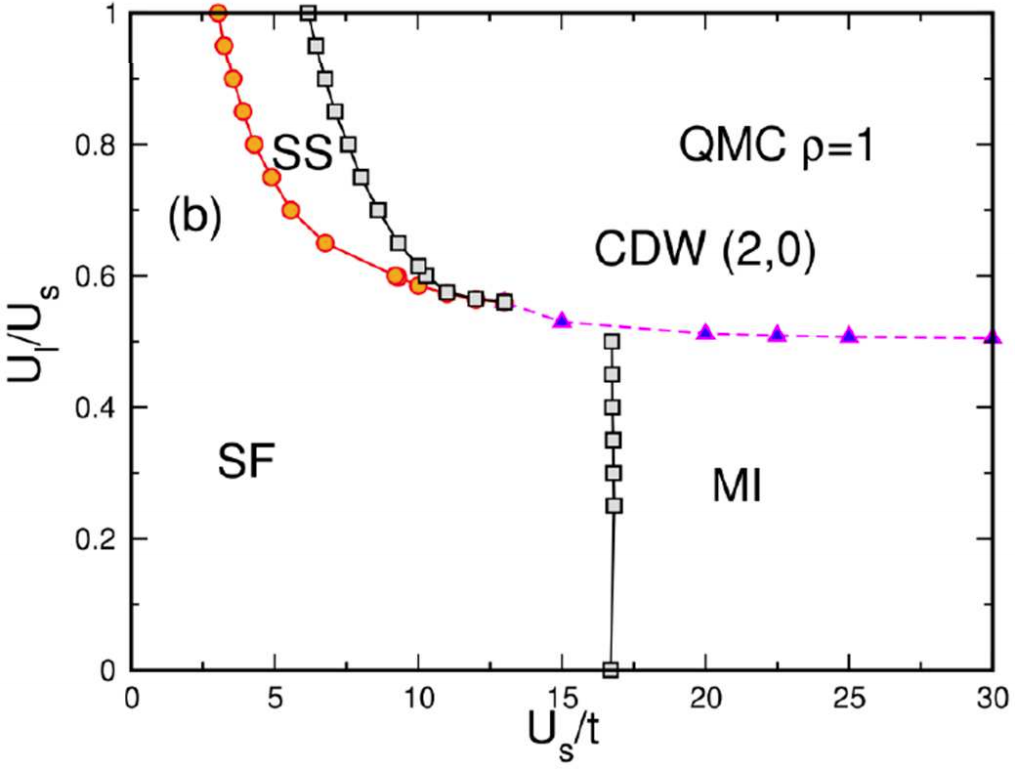
In this paper, we study the two-dimensional Bose-Hubbard model with short- and longrange interactions in the canonical ensemble. Using a Variational Monte-Carlo method, we obtain the phase diagrams containing four different phases: Mott insulator, density wave, superfluid and supersolid. The transition lines are determined using the structure factor and the superfluid density. We observe that the phase diagrams for short and long-range interactions are very similar quantitatively and qualitatively, but show also some significant differences. To evaluate the quality of our Variational approach, we compare our results with results published by other groups, obtained with various methods, such as an exact quantum Monte-Carlo algorithm and Gutzwiller Ansatz.







Quantum XX-model with competing short- and long-range interactions: Phases and phase transitions in and out of equilibrium

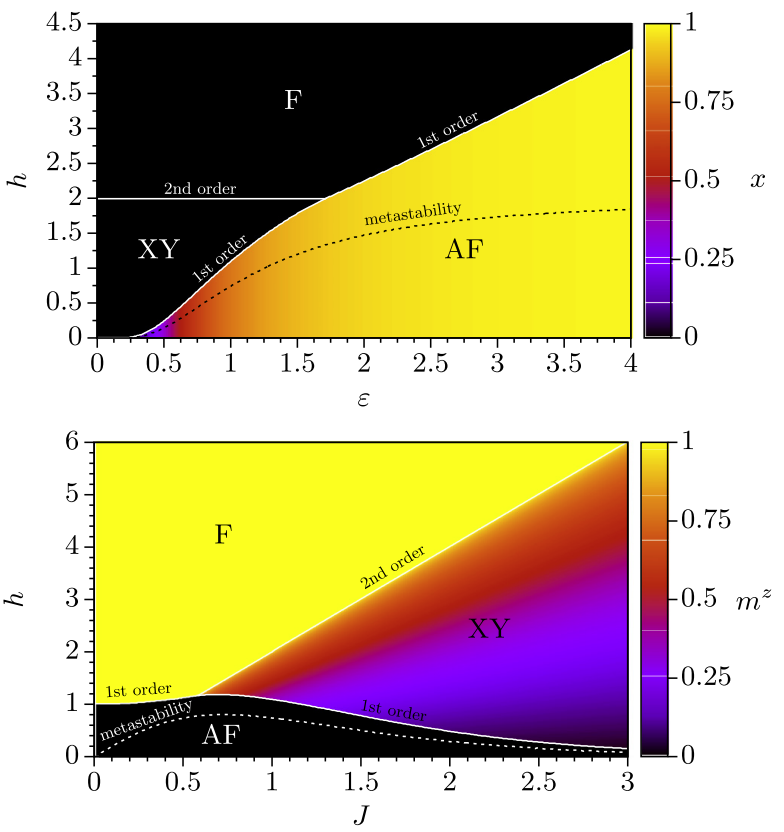
We consider the quantum XX model in the presence of competing nearest-neighbor and global-range interactions, which is equivalent to a Bose-Hubbard model with cavity mediated global-range interactions in the hard-core boson limit. Using fermionic techniques the problem is solved exactly in one dimension in the thermodynamic limit. The ground state phase diagram consists of two ordered phases: ferromagnetic (F) and antiferromagnetic (AF), as well as an XY phase having quasi-long-range order. We have also studied quantum relaxation after sudden quenches. Quenching from the AF phase to the XY region remanent AF order is observed below a dynamical transition line. In the opposite quench, from the XY region to the AF phase beyond a static metastability line AF order arises on top of remanent XY quasi-long-range order, which corresponds to dynamically generated supersolid state in the equivalent Bose-Hubbard model with hard-core bosons.









Quantum Relaxation and Metastability of Lattice Bosons with Cavity-Induced Long-Range Interactions

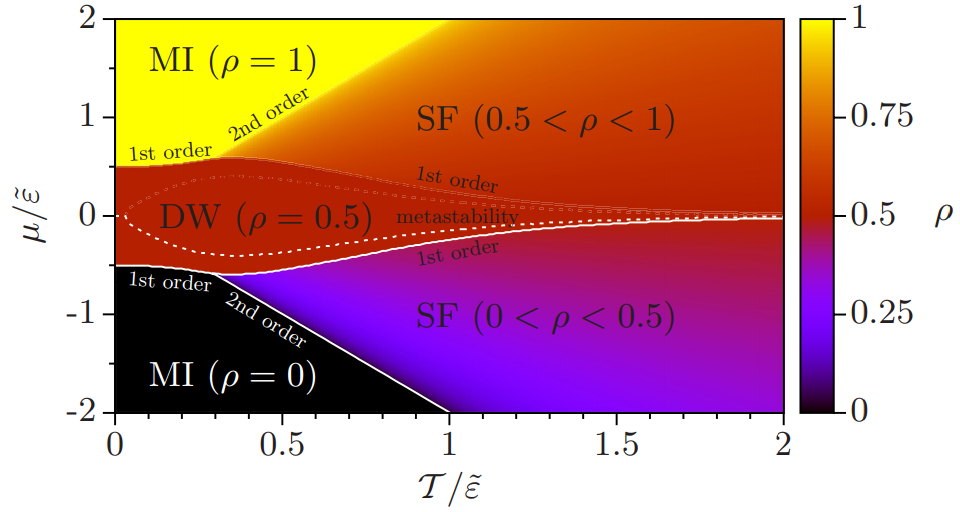
The coupling of cold atoms to the radiation field within a high-finesse optical resonator, an optical cavity, induces long-range interactions which can compete with an underlying optical lattice. The interplay between short- and long-range interactions gives rise to new phases of matter including supersolidity (SS) and density waves (DW), and interesting quantum dynamics.

Light cone in the two-dimensional transverse-field Ising model

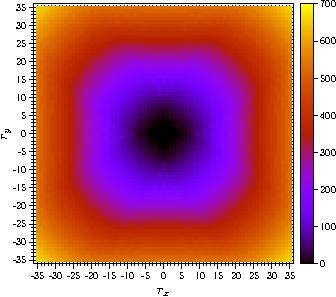
The propagation of a local perturbation through the transverse-field Ising model with nearest-neighbour interactions has a finite velocity, resulting in a light cone. Considering the Hamiltonian of the two-dimensional transverse-field Ising model one finds that the propagation of a local perturbation through the system has to respect its lattice structure. On the other hand one would expect a sufficiently large system to behave like a continuum at sufficiently large distances. We compute the time evolution of a local perturbation in the two-dimensional transverse-field Ising model with a time-dependent application of mean-field theory based on the BBGKY hierarchy to solve this apparent contradiction.

Thermalization in the two-dimensional transverse-field Ising model

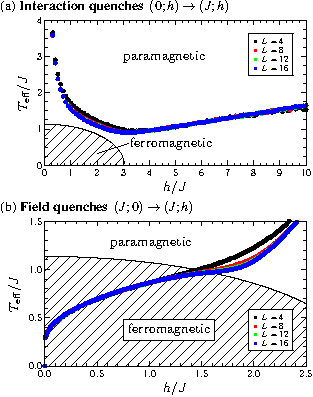
As the transverse-field Ising model on the two-dimensional square lattice is non-integrable, the total energy is the only conserved quantitiy under the unitary time evolution after a quantum quench, thus the system may thermalize. We apply real-time Variational Monte Carlo with suitable ansatz functions to compute the time evolution of the system after quenches of the coupling between the spins or of the external transverse field and check the system for thermalization comparing time-averages of the observables after the quenches to ensemble averages of the system in thermal equilibrium at a temperature defined by the quench parameters.

Test of quantum thermalization in the two-dimensional transversefield Ising model

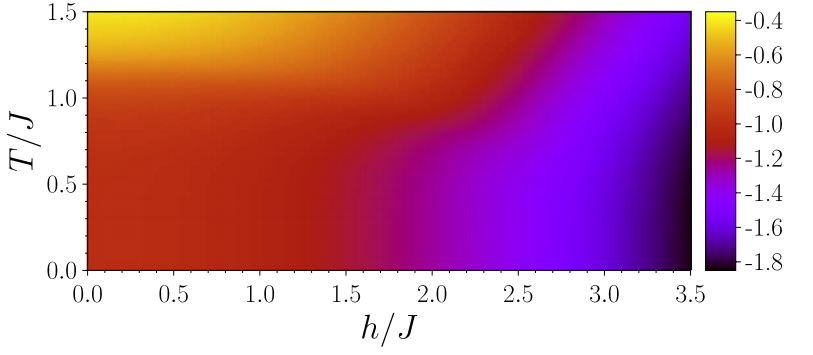
We study the quantum relaxation of the two-dimensional transverse-field Ising model after global quenches with a real-time variational Monte Carlo method and address the question whether this nonintegrable, two-dimensional system thermalizes or not. We consider both interaction quenches in the paramagnetic phase and field quenches in the ferromagnetic phase and compare the time-averaged probability distributions of non-conserved quantities like magnetization and correlation functions to the thermal distributions according to the canonical Gibbs ensemble obtained with quantum Monte Carlo simulations at temperatures defined by the excess energy in the system. We find that the occurrence of thermalization crucially depends on the quench parameters: While after the interaction quenches in the paramagnetic phase thermalization can be observed, our results for the field quenches in the ferromagnetic phase show clear deviations from the thermal system. These deviations increase with the quench strength and become especially clear comparing the shape of the thermal and the time averaged distributions, the latter ones indicating that the system does not completely lose the memory of its initial state even for strong quenches. We discuss our results with respect to a recently formulated theorem on generalized thermalization in quantum systems.









Ultracold Bosons with cavity-mediated long-range interactions: A local mean field analysis of the phase diagram

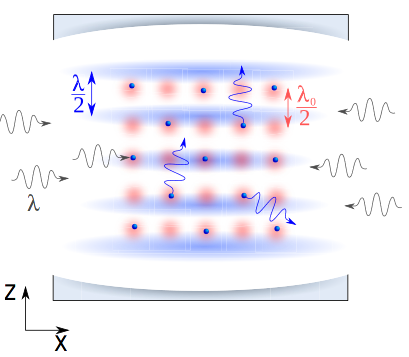
Ultracold bosonic atoms in optical lattices self-organize into a variety of structural and quantum phases when placed into a single-mode cavity and pumped by a laser. Cavity optomechanical effects induce an atom density modulation at the cavity-mode wavelength that competes with the optical lattice arrangement. Simultaneously short-range interactions via particle hopping promote superfluid order such that a variety of structural and quantum coherent phases can occur. We analyze the emerging phase diagram in two dimensions by means of an extended Bose-Hubbard model using a local mean-field approach combined with a superfluid cluster analysis. For commensurate ratios of the cavity and external lattice wavelengths, the Mott insulator-superfluid transition is modified by the appearance of charge density wave and supersolid phases, at which the atomic density supports the buildup of a cavity field. For incommensurate ratios, the optomechanical forces induce the formation of Bose-glass and superglass phases, namely, nonsuperfluid and superfluid phases, respectively, displaying quasiperiodic density modulations, which in addition can exhibit structural and superfluid stripe formation. The onset of such structures is constrained by the on-site interaction and is favorable at fractional densities. Experimental observables are identified and discussed.

Bosons in a bichromatic quasi-periodic potential: Analysis of the disorder in the Bose-Hubbard parameters and phase diagrams

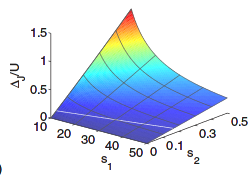
Experimental realizations of disorder in optical lattices generate a distribution of the Bose-Hubbard (BH) parameters, like on-site potentials, hopping strengths, and interaction energies. We analyze this distribution for bosons in a two-dimensional bichromatic quasiperiodic potential by determining the generalized Wannier functions and calculating the corresponding BH parameters. Using a local mean-field cluster analysis, we study the effect of the corresponding disorder on the phase diagrams. We find a substantial amount of disorder in the hopping strengths, which produces strong deviations from the phase diagram of the disordered BH model with purely random on-site potentials.

Quantum phase transition and correlations in the multi-spin-boson model

A continuous time cluster algorithm for two-level systems coupled to a dissipative bosonic bath is presented and applied to the sub-Ohmic spin-boson model. When the power s of the spectral function J(w) ∝ ws is smaller than 1/2, the critical exponents are found to be classical, mean-field like. Potential sources for the discrepancy with recent renormalization group predictions are traced back to the effect of a dangerously irrelevant variable.

Non-equilibrium quantum relaxation across a localization-delocalization transition

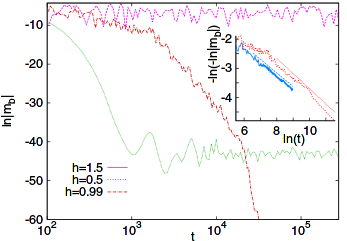
We consider the one-dimensional XX model in a quasiperiodic transverse field described by the Harper potential, which is equivalent to a tight-binding model of spinless fermions with a quasiperiodic chemical potential. For weak transverse field (chemical potential), h < h c , the excitations (fermions) are delocalized, but become localized for h > h c . We study the nonequilibrium relaxation of the system by applying two protocols: a sudden change of h (quench dynamics) and a slow change of h in time (adiabatic dynamics). For a quench into the delocalized (localized) phase, the entanglement entropy grows linearly (saturates) and the order parameter decreases exponentially (has a finite limiting value). For a critical quench the entropy increases algebraically with time, whereas the order parameter decreases with a stretched exponential. The density of defects after an adiabatic field change through the critical point is shown to scale with a power of the rate of field change and a scaling relation for the exponent is derived.

Superfluid clusters, percolation and phase transitions in the disordered, two dimensional Bose-Hubbard model

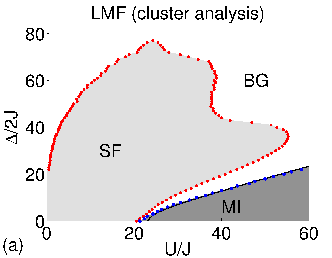
The Bose glass (BG) phase is the Griffiths region of the disordered Bose–Hubbard model (BHM), characterized by finite, quasi-superfluid clusters within a Mott insulating background. We propose to utilize this characterization to identify the complete zero-temperature phase diagram of the disordered BHM in d ≥ 2 dimensions by analysing the geometric properties of what we call superfluid (SF) clusters, which are defined to be clusters of sites with non-integer expectation values for the local boson occupation number. The Mott insulator phase then is the region in the phase diagram where no SF clusters exist, and the SF phase the region where SF clusters percolate—the BG phase is inbetween: SF clusters exist, but do not percolate. This definition is particularly useful in the context of local mean field (LMF) or Gutzwiller–Ansatz calculations, where we show that an identification of the phases on the basis of global quantities such as the averaged SF order parameter and the compressibility is misleading. We apply the SF cluster analysis to the LMF ground states of the two-dimensional disordered BHM to produce its phase diagram and find (a) an excellent agreement with the phase diagram predicted on the basis of quantum Monte Carlo simulations for the commensurate density n = 1 and (b) large differences to stochastic mean field and other mean field predictions for fixed disorder strength. The relation of the percolation transition of the SF clusters with the onset of non-vanishing SF stiffness indicating the BG to SF transition is discussed.

Quantum phases of incommensurate optical lattices due to cavity backaction

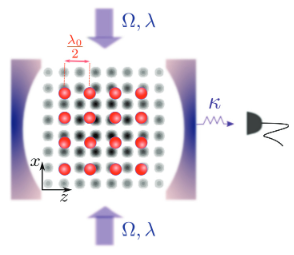
Ultracold bosonic atoms are confined by an optical lattice inside an optical resonator and interact with a cavity mode whose wavelength is incommensurate with the spatial periodicity of the confining potential. We predict that the intracavity photon number can be significantly different from zero when the atoms are driven by a transverse laser whose intensity exceeds a threshold value and whose frequency is suitably detuned from the cavity and the atomic transition frequency. In this parameter regime the atoms form clusters in which they emit in phase into the cavity. The clusters are phase locked, thereby maximizing the intracavity photon number. These predictions are based on a Bose-Hubbard model, whose derivation is reported here in detail. The Bose-Hubbard Hamiltonian has coefficients which are due to the cavity field and depend on the atomic density at all lattice sites. The corresponding phase diagram is evaluated using quantum Monte Carlo simulations in one dimension and mean-field calculations in two dimensions. Where the intracavity photon number is large, the ground state of the atomic gas lacks superfluidity and possesses finite compressibility, typical of a Bose glass.

Non-equilibrium quantum dynamics after local quenches

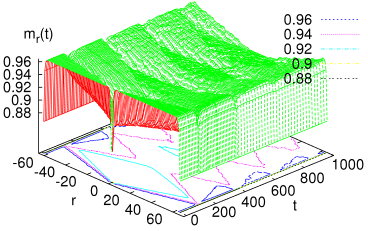
We study the quantum dynamics resulting from preparing a one- dimensional quantum system in the ground state of initially two decoupled parts which are then joined together (local quench). Specifically we focus on the transverse-field Ising chain and compute the time dependence of the magnetization profile, ml(l) , and correlation functions at the critical point, in the ferromagnetically ordered phase and in the paramagnetic phase. At the critical point we find finite-size scaling forms for the non-equilibrium magnetization and compare predictions of conformal field theory with our numerical results. In the ferromagnetic phase the magnetization profiles are well matched by predictions from a quasi-classical calculation that we describe.

Semi-classical theory for quantum relaxation in exactly solvable spin chains

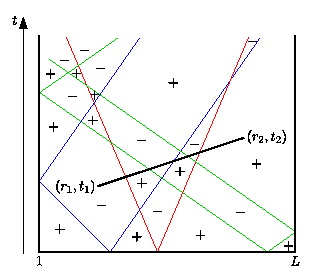
We use a semiclassical theory to explain the relaxation process in the one-dimensional transverse-field Ising and XY model after quantum quenches and compare the predictions of the semiclassical theory to exact results of free fermion techniques. The semiclassical theory gives both a quantitatively highly accurate as well as an illustrative description of the relaxation process. Its quasiparticles are kinks, which are created by the quantum quench and which travel ballistically through the chain with a constant velocity. They do not interact with each other and cause the relaxation process flipping a spin when they pass its position.

Legal notice (Impressum) Privacy policy